Gas Hydrate

The Langmuir adsorption coefficient is approximated from integration of a function which uses the Kihara cell potential (rather than the empiric procedure suggested by Parrish and Prausnitz (1972)).

In addition to the hydrate dissociation pressure the function calculates the water free hydrate composition and the fractional occupancy of each hydrate former in each hydrate cavity. The function also predicts which of the hydrate structures (only sI or sII) should be the most stable structure.

Note that the model is only applicable for describing the equilibrium of hydrate systems above the ice point temperature of water.

The van der Waals-Platteeuw model employs either CPA or the newly proposed qCPA as the thermodynamic model, which is used for fugacity and multiphase PT-flash calculations. The function is designed to work with the MATLAB CPA (or qCPA) MEX library (also introduced at the workshop), which gives access to both fugacity calculations as well as a fast and robust multiphase PT flash routine.

Essentially the same model has previously been implemented in FORTRAN by Peter Jørgensen Herslund (2013).

The main purpose of the new MATLAB implementation is:

1st) To make hydrate calculations more accessible and modifiable both to students and other professionals who may not be familiar with FORTRAN

2nd) To illustrate how the MATLAB MEX tool can be used for secondary developments in MATLAB, where the in-build optimization and graphical features of MATLAB can be utilized.

A minimal working example (MWE) of how the MATLAB function is employed to calculate the hydrate formation pressure for pure CO2 hydrates is shown below, including a figure with the modeling results compared to experimental data (the plot commands and data are not shown in the example).

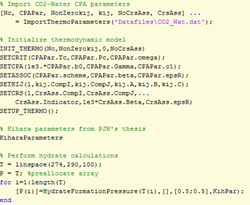
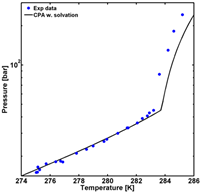
Figure 1 (Left) MWE of the needed code for calculation of the hydrate formation pressure of a binary mixture (CO₂ and water). (Right) Illustration of the (generated in MATLAB).